经过平衡二阶色散和非线fs的脉冲,而且设备相对简略。但是,受限于孤子面积理论,孤子能量无法逐渐提高。为客服这个约束,需求激发带啁啾的脉冲,但后续的紧缩使光路更为杂乱一起功率也将下降。因而,为了保存孤子
最近的几项研讨标明,在非线性和负四阶色散的平衡下存在纯四次孤子(Pure quartic soliton),其脉冲形状坚持不变。纯四次孤子具有能量扩展的优势,在短脉宽条件下能够取得更高能量的脉冲。科学家期望将这一发现过渡到现在很老练的光纤激光器中。但是,色散操控所需的制作工艺技能要求很严厉,如安在光纤中进行色散办理以完成四次孤子成为要处理的难题。
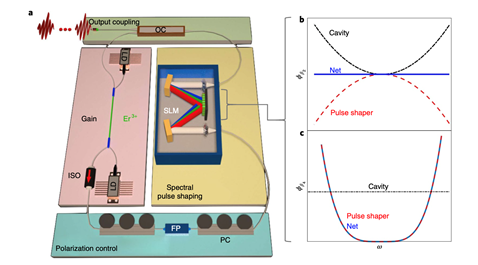
Runge等人使用光谱脉冲整形器完成了腔内的色散操控,初次在光纤激光器中取得了纯四次孤子[1]。设备如图1所示,掺铒光纤激光器选用非线性偏振旋转锁模机制,腔长21.4m,对应的基阶重复频率为9.3MHz。依据空间光调制器的可编程脉冲整形器能够发生恣意的相位操控腔内色散,主要有两个效果:(1)补偿腔内光纤引进的二阶和三阶色散;(2)供给很多的负四阶色散。
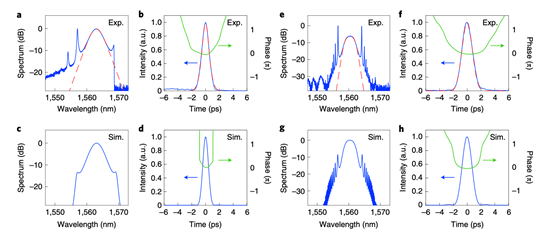
图2 试验上和理论上惯例孤子(abcd)和纯四次孤子(efgh)的光谱和时域曲线
脉冲整形器不供给相位补偿时,激光器作业在惯例孤子区域,试验和理论模仿成果如图2(a-d)所示,脉冲的中心波长为1563nm,光谱宽度3.72nm,脉冲宽度为1.23ps,具有凯利边带,为典型的惯例孤子。使用脉冲整形器补偿相位并引进很多负四阶色散后,试验和理论模仿成果如图2(e-h)所示,脉冲的光谱宽度为3.16nm,脉冲宽度为1.74ps,稍带啁啾。与惯例孤子比较,纯四次孤子光谱的中心处愈加平整,而且具有较强的窄间隔光谱边带。
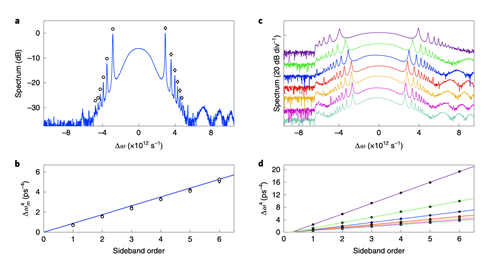
与惯例孤子类似,纯四次孤子在谐振腔中传达时遭到扰动发生这些边带。当纯四次孤子和边带的传达常数满意相长干与时,会导致光谱峰变窄。关于四阶色散腔中传达的线性波而言,第m阶共振峰满意以下联系:
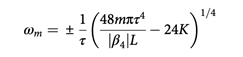
试验大将边带频率的四次方和其阶次对应,如图3b所示,发现满意线性联系,与理论契合。而且,改动四阶色散的值,依然满意线d所示。
考虑到惯例孤子激光器的能量约束,作者研讨了四阶孤子脉冲能量和脉冲宽度的联系,理论和数值模仿标明,四阶孤子能量由下式决议:
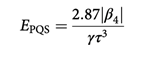
纯四次孤子能量与脉冲宽度的三次方成反比。改动输入功率,对除掉边带部分光谱进行积分得到脉冲能量,依据时刻带宽积0.67得出脉冲宽度。
考虑到纯四次孤子和惯例孤子物理的类似性,同年,Runge等人理论上研讨了脉冲在包括正四阶色散和增益的介质中的自类似传达[2]。在四阶正色散情况下,脉冲向新的渐进解演化,其时域和频域曲线与二阶色散情况下明显不同。理论依据成果得出,跟着传输间隔添加,脉冲坚持其形状不变,强度与T^{4/3}成正比,瞬时频率和T^{1/3}成正比。该自类似脉冲的宽度和强度都呈指数添加,而且总增益的3/7用于添加脉冲宽度,4/7用于添加脉冲强度。
脉冲在介质中传达时,因为非线性效应会发生新的频率成分。一般,脉冲的前沿红移,脉冲的后沿蓝移。关于自类似脉冲而言,其瞬时频率正比于T^{1/3},即瞬时频率的3次方正比于时刻T(△ω3∝T)。别的,在只要四阶色散情况下,群延时\beta_1与频率改变的三次方成正比(\beta_1=\beta_4△ω3)。所以,部分群延时与时刻T呈线形联系。成果是脉冲在传达过程中坚持T^{4/3}的强度散布不变。
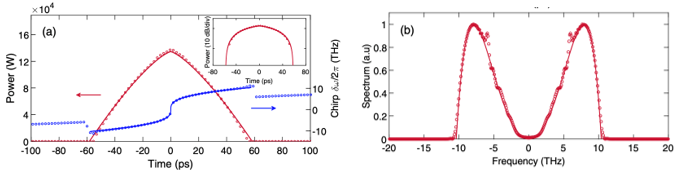
图4 理论和模仿自类似演化输出时域曲线和频域曲线实线:理论成果;圆圈:数值模仿成果
为了验证理论估测,作者依据分步傅里叶法模仿了脉冲的演化,模仿成果与理论估测十分符合(如图4所示)。脉冲光谱如图4b所示,出现双峰结构。而且因为色散为正,脉冲的前沿蓝移,脉冲的后沿红移。
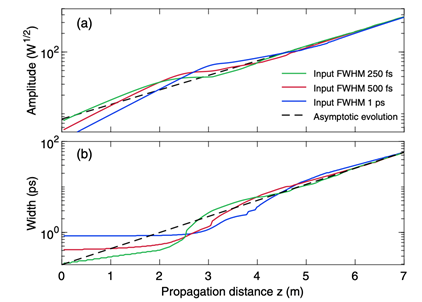
图5为不同脉冲宽度下振幅和脉冲宽度随传达间隔的演化,标明四阶色散中的自类似脉冲的振幅和脉宽与入射脉冲形状和入射脉冲宽度无关。这与二阶色散情况下共同。
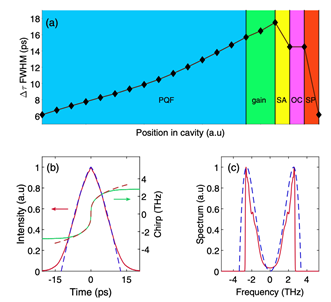
依据正四阶色散中的自类似演化,作者模仿了一台激光器体系,如图6a所示,腔内包括7m长的无源四阶色散光纤、1m长的有源四阶色散光纤、可饱和吸收体、输出耦合器和滤波器。输出脉冲形状和光谱如图6b和6c所示,时域上为三角形脉冲,频域上为双峰结构,模仿成果与理论剖析彻底匹配。
上述两项作业研讨了四阶色散和克尔非线性的相互效果,标明纯四次孤子和四阶自类似脉冲与传统的孤子和自类似在物理上具有类似性,为孤子能量和脉冲宽度扩展以及自类似的发生供给了新的自由度,在超快光纤激光器、片上频率梳、超接连发生等方面有重要意义。


